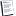
Если быть точным, то (квадратный корень из 3) * 25 кВ = 43,3 кВ.
А для комнатных 220В между фазой и нулём - межфазное напряжение получится 380В, знакомая цифра?
На самом деле тут одной цифрой не обойтись. На вопрос "почему" без лекции на тему электротехники вообще затрудняюсь объяснить, но попробую: итак, у нас есть три фазы. Для каждой существует график зависимости напряжения от времени: синусоида с периодом 1/50 секунды и амплитудой - нет, не 25 кВ, а (корень из 2) * 25 кВ = 35,4 кВ.
Сделана такая амплитуда вот зачем: мощность потребителя с чисто активным сопротивлением = U^2/R, если построите график мощности от времени, получится синусоида в квадрате, где мощность меняется от нуля до значения когда амплитудное значения напряжения подставить в последнюю формулу. А средняя мощность за период - в точности половина от максимальной мощности. Так вот, исторически сложилось, что электротехникам гораздо удобнее назвать напряжением переменного тока не амплитуду напряжения, а как раз такую цифру, которая бы позволила получить аналогичную мощность на постоянном напряжении.
То есть напряжение, периодически меняющееся по гармоническому закону (=по синусоиде) от минус 35,4 кВ до плюс 35,4 кВ, электротехники договорились называть напряжением 25 кВ, просто потому, что постоянное напряжение в 25 кВ будет обеспечивать потребителю такую же мощность.
Итак, поехали дальше. У нас три фазы - три синусоиды с одной амплитудой, но смещённые по фазе (собственно, поэтому их и назвали фазами) на 120 градусов (просто поровну поделили 360 градусов на три).
Посчитайте теперь разность между двумя любыми фазами. Это будет тоже синусоида, но с фазой, лежащей "посередине" между выбранными синусоидами и амплитудой, большей в корень из 3 раз (если правильно помню - складывать синусоиды учат ещё в школе).
Получается, что в какие-то моменты периода мгновенная разность напряжений между фазами составит 25 кВ * корень 2 * корень 3 = 61,2 кВ.
p.s. плохо дома болеть гриппом - столько свободного времени на болтовню...
|